Into the Void: An Introduction to Orbital Dynamics
How does space travel work? What are the constraints of movement in space? Gravity, orbital motion and its characteristics.

An Introduction to Orbital Dynamics
Outer space, unlike Earth, appears as a shapeless void, devoid of familiar features such as mountains, valleys, or rivers.
Yet, what distinguishes space is not what meets the eye; rather, it is the invisible forces that govern it: radiation, energy, and gravity.
Among these forces, gravity stands out as the primary orchestrator of motion in outer space. Just as wind and currents shape movement in the ocean, gravity creates “a certain ‘topography’ of gravitational mountains and valleys”, influencing the trajectories of objects traversing the cosmos. (MacDonald, 2007, p.599).
...
This is the first in a series of articles called Into the Void, which defines the rules governing the space domain, substantially different from those on Earth - such as the laws of orbital mechanics that govern motion.
The series aims to lay the basis for understanding the constraints posed by the very nature of the space environment that must be considered when planning how to ensure its security.
- This very first article begins by comprehending the effect of gravity on space motion.
- It will then introduce the orbits, which may be considered space highways, where motion is easier, less energy-demanding, and thus cheaper.
- It then concludes with the characteristics that differentiate one orbit from another: its period, altitude, eccentricity and orbital plane.
1. Gravity
While in terrestrial travel movement is influenced primarily by the gradient, in space, it is gravity that plays the key role in determining motion.
“The unseen undulations of outer space terrain, the hills and valleys of space, are more properly referred to as gravity wells” (Dolman, 2005, p.62).
If one were to visually represent the force of gravity, as we would do with mountains or valleys for Earth, this would act as a sinking weight on a flexible sheet (Figure 1). The greater the mass of an object, the more powerful its gravitational pull and the more profound the gravitational well it forms.
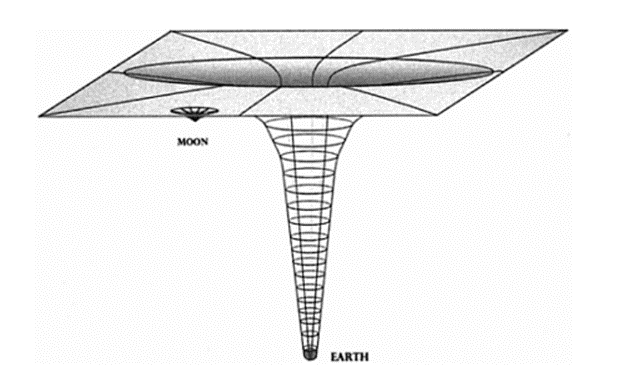
“The earth’s well is twentytwo times deeper than the moon’s”(Ra’anan & Pfaltzgraff, 1984, p.35).
Therefore, the linear distance of two points is of little importance when planning a movement in space.
- This means that it requires much more energy to reach an orbit 36 000 km from the Earth (geosynchronous orbit) if one departs from Earth than departing from the Moon – even though the distance of such an orbit from the Moon is 348,000 km (In-Depth | Earth’s Moon, n.d.).
- Similarly, reaching Mars from the Moon, when this is at the closest orbital point to the Red Planet (56 million km), requires less energy than reaching the Moon from Earth (just 384,000 km) (Dolman, 2005, p.62).
What becomes important in space is the change in velocity needed to move between two points, not the distance between them, as it is the change in velocity that determines the cost of spatial transport (Ra’anan & Pfaltzgraff, 1984, p.35).
Along these lines, space behaves somewhat like the open sea, which, although it can be navigated in any direction, creates more convenient routes arising from sea currents and winds.
Similarly, in space, due to gravity, there are specific orbits or transit routes on which space travel is more convenient as a result of the fuel efficiency advantage and other routes that are impossible because of the prohibitive propellant consumption costs (Dolman, 2005, p.63).
In addition, in space, there is no air resistance slowing down the moving object, and when even the force of gravity is absent, no forces are acting on the object, allowing it to maintain its speed without needing any additional propellant.
One of the routes where the propellant consumption of an object is zero, despite being in motion and gravity’s influence, is that of orbits.
2. The Orbits
There are two ways to understand the functioning of orbits.
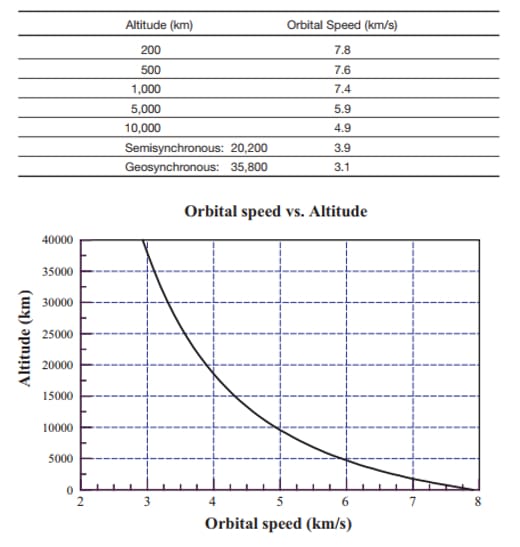
An orbiting satellite is subjected to two forces acting on it: the centrifugal force and the force of gravity. “At the proper speed, the centrifugal force of the satellite due to its motion around the Earth just balances the pull of gravity, and the satellite remains in orbit” (Wright et al., 2005, p.20). The relationship between speed and centrifugal force is direct: as one increases, the other increases as well.
It follows that farther orbits will have a lower orbital speed, and closer orbits will need a higher speed.
- If the specific speed for which the centrifugal force equals the force of gravity were exceeded (i.e., escape velocity), the satellite would move away from Earth and be lost in space.
- Similarly, if the speed were even slightly slower than the target speed, the satellite would fall back to Earth.
Alternatively, it can be considered as if the satellite is constantly falling towards the Earth, but since it is moving parallel to it and the Earth is curving away from the satellite, the latter never falls (Figure 3).
“The phenomenon that a satellite in orbit expends no fuel or energy is due to the fact that the satellite is constantly falling toward the body it orbits” (Dolman, 2005, p.53).



Figure 3. Explanation of orbital motion by Isaac Newton: the Cannonball. [Source: Chapter 3: Gravity & Mechanics. (n.d.). NASA. Retrieved 11 March 2024, from https://science.nasa.gov/learn/basics-of-space-flight/chapter3-4/]
It is also important to emphasise that “the speed needed to keep a satellite in orbit does not depend on the mass of the satellite” on the fundamental principle that “the trajectory of an object in the vacuum of space does not depend on its mass” (Wright et al., 2005, p.21).
Therefore, the speed the satellite must maintain depends only on the altitude of its orbit. Once accelerated to its orbital velocity by a rocket, the satellite no longer needs to be accelerated to stay in orbit.
3. Period, Altitude and Eccentricity
Having defined the orbit as “the path of a spacecraft or satellite caught in the grip of gravity”, its period is referred to as the time it takes the satellite to make one complete revolution around the Earth, and thus complete one orbit (Gray & Sloan, 1999, p.84).
“An orbit is described first in terms of altitude (above the surface of the orbited body) and eccentricity (or variation in altitude)” (Dolman, 2005, p.53), which determines whether the orbit is circular (zero or close to zero eccentricity) or elliptical (Figure 4).
The point at which the satellite is farthest from Earth, i.e., maximum altitude, is called apogee, conversely, the closest point, i.e., minimum altitude, is called perigee.

In concentric orbits, as the altitude increases and the satellite’s speed decreases, the orbital period increases. As altitude decreases, orbits suffer more from interference from atmospheric density and gravitational fluctuations. Consequently, orbits with a higher altitude are more stable orbits.
- Perturbations in the satellite's circular orbit reach a critical effect when its period is less than 93 minutes, as they would require an excessive amount of fuel to perform orbital corrections of spacing, distance and speed.
- Similarly, orbits of less than 160 km altitude (87.5 min) are not practically sustainable due to atmospheric drag (Dolman, 2005, p.56).
However, no orbit is perfect, since even increasing the altitude of the orbit, increasingly significant perturbations come into play, such as “the gravitational fields of the sun, moon, and other celestial bodies, and the effects of solar radiation including solar flares, and the impacts of meteors and debris that strike the satellite at hyper-velocity”, which require fuel consumption to perform orbital corrections (Dolman, 2005, p.56)
4. The Orbital Plane
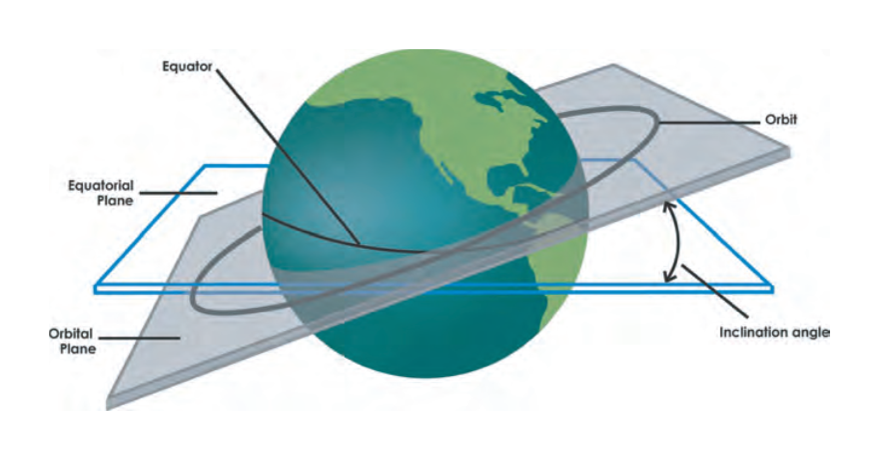
Describing the orbital plane as the imaginary plane on which the orbit lies and the equatorial plane as the equator one, the inclination of the orbit is defined as the angle created by the intersection of the two planes, and the points where the orbit crosses the equatorial plane are defined as nodes (Figure 5).
- When the inclination angle of the orbit is 90° it passes through the poles, i.e., polar orbit.
- When the angle is 0° the orbit is perfectly coincident with the equatorial plane and has no nodes.
The satellite at an altitude of 36,000 km orbits once a day (Geosynchronous orbit).
If this satellite, rotating at the same rate as Earth, travels in an equatorial orbit, it will always be above the same point of the Earth (Geostationary orbit).
📌 Key Takeaways
- Outer space is characterized by invisible forces such as radiation, energy, and gravity, which govern motion. Gravity creates gravity wells, influencing movement similarly to wind and currents in the ocean. Consequently, movement in space mainly depends on gravity, not distance, and requires energy to counteract its effects.
- Orbits are crucial in space travel, with orbital speed determined by the balance of centrifugal force and gravity. Perturbations from celestial bodies, solar radiation and Earth's atmosphere necessitate fuel consumption for orbital corrections.
- Orbits are defined by period, altitude, and eccentricity. Orbital inclination and nodes define the orientation of an orbit, with polar and equatorial orbits being extremes.
- Geosynchronous and geostationary orbits are orbits with specific characteristics: the former completes one orbit around the Earth daily, while the latter remains stationary relative to the Earth's surface while orbiting once a day.
References 📃
- Dolman, E. C. (2005). Astropolitik: Classical geopolitics in the space age. Routledge.
- Gray, C. S., & Sloan, G. (1999). Geopolitics, Geography, and Strategy. Frank Cass.
- In Depth | Earth’s Moon. (n.d.). NASA Solar System Exploration. Retrieved 8 February 2023, from https://solarsystem.nasa.gov/moons/earths-moon/in-depth.
- MacDonald, F. (2007). Anti-Astropolitik - Outer space and the orbit of geography. Progress in Human Geography, 31(5), 592–615.
- Ra’anan, U., & Pfaltzgraff, R. L. (1984). International security dimensions of space (Fletcher School of Law and Diplomacy, Ed.). Archon Books.
- Wright, D., Grego, L., & Gronlund, L. (2005). The physics of space security. A Reference Manual.

